Duas pessoas iniciam de um mesmo ponto um passeio com percursos distintos. Uma delas vai correndo e o seu trajeto segue a curva da função f(x) = -x2 + 20x e a outra pessoa vai andando seguindo o traçado da função g(x) = 2x. Elas marcaram de se encontrar no ponto que é a origem do Plano Cartesiano. Qual foi o ponto de partida destas pessoas?
Neste problema temos duas funções conhecidas. f(x) é uma função quadrática e g(x) é uma função linear. Ambos os tipos de função já foram estudados aqui no Matemática Didática.
Este problema se interessa pelos pontos que são comuns às duas funções. O ponto (0, 0) já foi informado, ele é a origem do Plano Cartesiano. O outro ponto é o que precisamos descobrir.
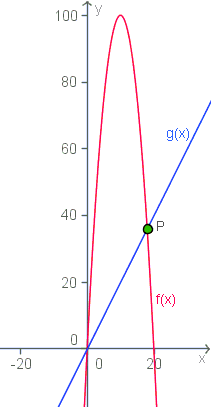
Embora o mesmo não seja necessário para solucionarmos este problema, o gráfico ao lado nos ajuda a ter uma visão melhor das informações que nos foram fornecidas pelo enunciado.
O gráfico da função f(x) é uma parábola visto que f(x) é uma função do segundo grau.
O gráfico da função g(x) é uma reta que passa pela origem porque g(x) é uma função linear.
O ponto P é o ponto de partida que estamos procurando, isto porque além do ponto (0, 0) que é o ponto de chegada, o ponto P é o único ponto comum às duas funções e as duas pessoas partiram de um mesmo ponto com destino ao ponto (0, 0).
Para solucionarmos o problema precisamos igualar as duas funções e calcular as suas raízes. Uma delas será abscissa do ponto (0, 0) e a outra a abscissa do ponto P:
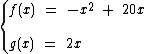
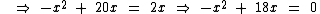
Esta é uma equação do segundo grau incompleta com c = 0 solucionada assim:
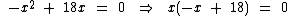
Para x1 temos:
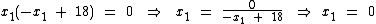
Para x2 temos:
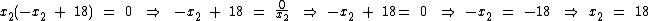
x1 = 0 é a abscissa do ponto (0, 0), o ponto de encontro.
x2 = 18 é a abscissa do ponto P. O valor da ordenada pode ser obtido substituindo x por 18 em f(x) ou em g(x). Vamos substituí-lo nas duas funções para que você possa verificar.
Substituindo em f(x) temos um processo mais trabalhoso:
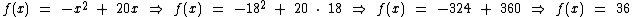
Já substituindo em g(x) chegamos ao mesmo resultado mais facilmente:
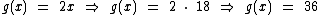
Portanto (18, 36) são as coordenadas do ponto P.
(18, 36) foi o ponto de partida destas pessoas.
