Um determinado jogo contém sessenta números inteiros distintos que variam de 1 a 60. A cada concurso são sorteados 6 destes números. Em cada aposta você pode escolher de 6 a 15 números distintos. Se você fizer uma aposta com 11 números, qual a probabilidade de acertar 4 dos 6 números que serão sorteados?
Tópico relacionadoFatorial
Na resolução deste problema iremos recorrer várias vezes à fórmula de cálculo da combinação simples que já estudamos no artigo Análise Combinatória - Combinação Simples:
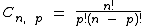
Em caso de dúvidas consulte o referido artigo para maiores informações.
Segundo o enunciado temos que acertar 4 dentre os 11 números escolhidos, o que resulta em 330 combinações possíveis:
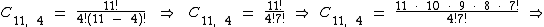
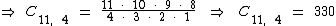
Como são sorteados 6 números em cada sorteio e foi realizada um aposta com 11 números, destes onze 4 são acertos, logo há mais 2 números errados dentre os 49 números restantes, o que totaliza 1.176 combinações distintas:
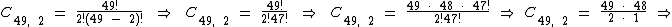
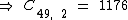
Portanto temos um total de 388.080 combinações possíveis, onde dos 11 números escolhidos acertamos 4 e erramos 2:
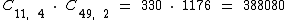
Para podermos obter a probabilidade solicitada, precisamos primeiramente calcular a combinação simples de 60 números combinados 6 a 6:
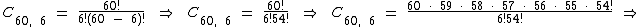
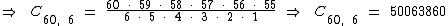
Logo, há 50.063.860 resultados possíveis ao se sortear 6 números dentre os 60.
Agora já temos como calcular a probabilidade de acertar 4 dos 6 números que serão sorteados:
Como é possível se obter 50.063.860 resultados distintos ao se sortear 6 números dentre 60 disponíveis, a probabilidade de acertar 4 dos 6 números que serão sorteados é de 252 chances em 32509, ou aproximadamente 1 chance em 129:
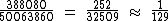
Note que foi preciso calcular C49, 2, pois serão acertados apenas quatro números dos seis a sortear. Se fossem acertados todos os seis, o cálculo se resumiria a:
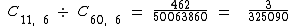
3/325090 equivale a aproximadamente uma chance em 108.363:
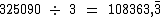
Vejamos um outro exemplo:
Um determinado jogo contém oitenta números inteiros distintos que variam de 1 a 80. A cada concurso são sorteados 5 destes números. Em cada aposta você pode escolher de 5 a 7 números distintos. Se você fizer uma aposta com 7 números, qual a probabilidade de acertar 3 dos 5 números que serão sorteados?
Para facilitar os cálculos vamos utilizar esta fórmula:
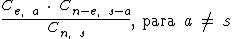
Onde:
e = 7, a quantidade de números escolhidos;
a = 3, a quantidade de acertos;
n = 80, o total de números e
s = 5, a quantidade de números sorteados.
Substituindo todos estes dados na fórmula:
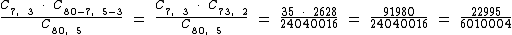
22995/6010004 equivale a aproximadamente uma chance em 261:
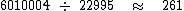
A fórmula mostrada acima pode ser utilizada quando nem todos os números sorteados foram acertados (a ≠ s). Quando acerta-se todos os números sorteados deve-se utilizar esta outra fórmula:
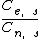
Voltando ao problema original, sua resposta é:
A probabilidade de acertar 4 dos 6 números que serão sorteados é 252/32509 ou aproximadamente 1/129.
