Função
O estudo do produto cartesiano serviu de base para aprendermos sobre as relações. Estas agora são o alicerce para o estudo das funções, por isto, para que você assimile melhor este conceito, é importante que você revise os tópicos sobre produto cartesiano e relações.
As funções nada mais são que um tipo particular de relação que possuem uma propriedade específica.
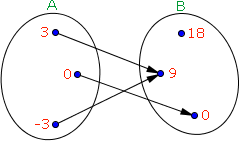
Para iniciarmos o estudo das funções vamos começar analisando a relação 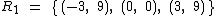 , cujo diagrama de flechas pode ser visto ao lado:
, cujo diagrama de flechas pode ser visto ao lado:
Observe que todos os elementos do conjunto A possuem uma flecha em direção a um único elemento do conjunto B.
Em outras palavras, não há no conjunto A qualquer elemento que não esteja associado a um elemento do conjunto B e os elementos de A estão associados a apenas um elemento de B.
Por possuir tal propriedade, dizemos que esta relação é uma função f de A em B representada por:
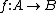
Domínio da Função
Ao conjunto A damos o nome de domínio da função.
O domínio é o conjunto de partida. Ele composto de todos os elementos do conjunto de partida.
Neste nosso exemplo o domínio da função f é representado por D(f) = { -3, 0, 3 }, ou seja, o domínio desta função contém todos os elementos do conjunto A.
Como supracitado, para que tenhamos uma função, todos os elementos do domínio devem estar associados a um e somente um dos elementos de B.
Contradomínio da Função
Ao conjunto B damos o nome de contradomínio da função.
O contradomínio é o conjunto de chegada. Ele composto de todos os elementos do conjunto de chegada.
Em nosso exemplo o contradomínio da função f é representado por CD(f) = { 0, 9, 18 }, isto é, o contradomínio desta função contém todos os elementos do conjunto B.
Segundo o conceito de função não é necessário que todos os elementos de B estejam relacionados aos elementos do domínio. Note que no conjunto B o elemento 18 não recebe nenhuma flecha, isto é, não está relacionado a qualquer elemento de A.
Uma outra coisa que deve ser observada é que em uma função os elementos do contradomínio podem receber mais de uma flechada, se associando, portanto, a mais de um elemento do domínio. Como exemplo temos o elemento 9 que está associado aos elementos do domínio -3 e 3.
Imagem da Função
A imagem da função dependendo do caso é o próprio contradomínio, ou então é um subconjunto seu.
Os elementos do conjunto imagem são todos os elementos do contradomínio que estão associados a algum elemento do domínio. No exemplo que estamos utilizando o conjunto imagem é representado por Im(f) = { 0, 9 }, pois 0 e 9 são todos os elementos do CD(f) que estão associados a algum elemento do D(f).
Em resumo para a função de exemplo temos:
Domínio da Função: D(f) = { -3, 0, 3 }
Contradomínio da Função: CD(f) = { 0, 9, 18 }
Conjunto Imagem da Função: Im(f) = { 0, 9 }
Nesta função exemplo o conjunto imagem é um subconjunto do contradomínio, pois o elemento 18 de B não está contido no conjunto imagem, por não estar associado a nenhum elemento do domínio.
Definição de uma Função
Esta função f de A em B, 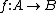 , é definida como:
, é definida como:
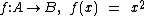
Ou ainda como:
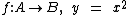
Veja também que representamos f(x) ou y em função de x. A variável f(x) ou y é chamada de variável dependente, pois depende de x, já a variável x é chamada de variável independente, pois independentemente de y, pode representar qualquer elemento do domínio.
A definição da função leva em conta tanto o domínio quanto do contradomínio, relacionando-os. O conjunto imagem Im(f), depende não só da regra de associação, no caso f(x) = x2, como também do D(f) e do CD(f).
Omissão do Domínio e do Contradomínio na Definição de uma Função
É provável que em muitos livros e em outros sites você tenha encontrado a definição de muitas funções, nas quais não foram feitas menções nem ao domínio, nem ao contradomínio das mesmas.
É que nestes casos se assume que o contradomínio seja o conjunto dos números reais, 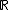 .
.
Mas qual será o domínio?
Isto depende da regra de associação em si, por isto vamos tomar como exemplo a seguinte função:
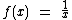
O contradomínio é:
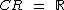
O domínio é o próprio conjunto dos números reais, desconsiderando-se os elementos para os quais 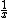 não seja um número real.
não seja um número real.
Como sabemos não existe um quociente real resultante da divisão por zero. Em outras palavras, se x = 0, isto é, se o domínio considerar o elemento 0, não existirá um elemento no contradomínio que possa ser associado a x, elemento este que deve pertencer a Im(f). Pela definição de função todo elemento do domínio deve possuir uma imagem.
Então devemos desconsiderar o número 0 e mais nenhum outro, pois a divisão de 1 por qualquer outro número real produz um quociente real.
O domínio desta função pode então ser definido por:
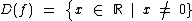
Ou ainda pelo conjunto dos números reais desconsiderando-se o zero:
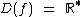
Logo a definição desta função poderia ser:
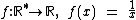
No caso da função 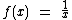 é muito fácil de se identificar que x não pode ser igual a 0, mas e no caso da função abaixo?
é muito fácil de se identificar que x não pode ser igual a 0, mas e no caso da função abaixo?
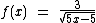
Bom, neste caso pelo mesmo motivo da função anterior o denominador da fração não pode ser igual a zero, além disto o radicando no denominador não pode ser negativo, pois não existe raiz quadrada real de número negativo, então concluímos que 5x - 5 deve ser maior que zero. Então temos:
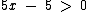
Isolando x no primeiro membro:
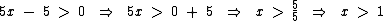
Portanto x deve ser maior que 1, pois se x for igual 1 teremos uma divisão por zero e se x for menor que 1 teremos um radical negativo. Podemos então definir o domínio desta função por:
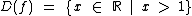
Desta forma podemos então definir assim esta função:
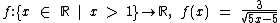
Não há como negar que 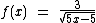 é uma forma bem mais simples de se definir esta função, é por isto que os livros costumam fazer assim.
é uma forma bem mais simples de se definir esta função, é por isto que os livros costumam fazer assim.
Exemplos de Relação que não é Função
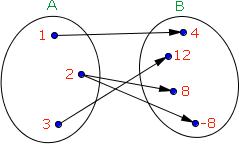
Observe o diagrama de flechas ao lado:
Ele não representa uma função de A em B, pois o elemento 2 do conjunto A possui duas imagens, -8 e 8, o que contraria o conceito de função.
Se apenas 8 ou -8 recebessem um flechada de 2, aí sim teríamos uma função.
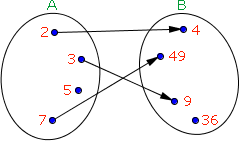
Agora vejamos este outro diagrama de flechas a seguir:
Veja que não há nenhum elemento do domínio que fleche mais de um elemento do contradomínio, mas ainda assim não estamos diante de uma função. Por quê?
Simplesmente porque o elemento 5 do conjunto A não possui uma imagem em B.
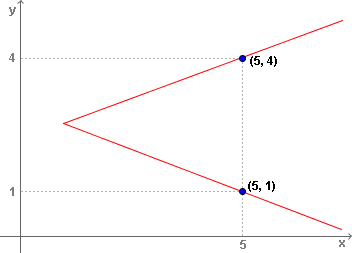
Observe agora o seguinte gráfico no plano cartesiano:
Ele representa ou não uma função?
Como sabemos, em uma função cada elemento x do domínio deve estar relacionado a um único elemento y do contradomínio, ou seja, deve possuir uma única imagem.
Note porém que neste gráfico os pontos (5, 1) e (5, 4), possuem a mesma abscissa, o que significa dizer que o elemento 5 do domínio possui duas imagens, ele flecha tanto o elemento 1, quanto o elemento 4 do contradomínio, portanto tal gráfico não representa uma função.
Em resumo, levando-se em conta o domínio e o contradomínio da relação, se no gráfico for possível traçar uma reta paralela ao eixo das ordenadas que passe por mais de um ponto do gráfico, ou ainda que não passe por nenhum dos seus pontos, então estaremos diante de um gráfico que não representa uma função.
Zeros ou Raízes de uma Função
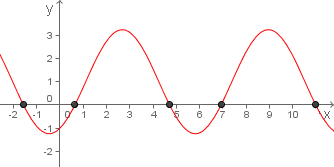
Olhe o gráfico da função ao lado e perceba que alguns dos seus pontos estão localizados sobre o eixo das abscissas.
A abscissa de cada um destes pontos é denominada zero da função ou raiz da função.
Todo elemento do domínio da função que tem como imagem o elemento 0, é uma raiz da função.
Os elementos do domínio que anulam a função são as suas raízes, isto significa dizer que dependendo da função, ela pode não possuir raízes reais, pois pode não existir no seu domínio nenhum elemento que a anule e sendo assim o seu gráfico nunca intercepta o eixo x, assim como também pode possuir infinitas raízes reais, pois o seu gráfico intercepta o eixo x infinitas vezes, já que podem existir infinitos elementos do seu domínio que tornem a função nula.
