Quando tratamos as porcentagens vimos como realizar um acréscimo percentual.

Vamos supor que uma pessoa, cujo salário mensal seja de R$ x, tenha obtido um reajuste salarial de 8,75%, então após este reajuste o salário desta pessoa passou a ser de R$ 1,0875x:

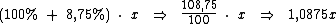
Na linguagem das funções se chamarmos de f a função que acrescenta o percentual de 8,75% ao salário, podemos assim defini-la:

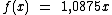
Agora vamos dizer que após alguns meses esta pessoa obteve um outro aumento salarial, desta vez de 10%.

Se novamente atribuirmos a variável x ao valor do salário sem este novo reajuste, o novo salário será calculado por:

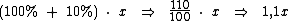
Que ao trabalharmos com funções, utilizando a letra g para representá-la, transcrevemos como:

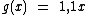
Se a pessoa antes do primeiro reajuste salarial recebia R$ 1.000,00 por mês, utilizando tais funções, qual seria o novo salário após o segundo reajuste?

Vamos ao cálculo do primeiro reajuste salarial:

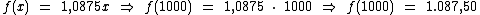
Então já que a pessoa passou a perceber R$ 1.087,50 mensais, então após o segundo reajuste o novo salário será:

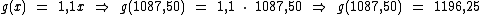
Portanto a pessoa percebia R$ 1.000,00 inicialmente, quando após um reajuste de 8,75% passou a ter um salário de R$ 1.087,50 e com um novo reajuste de 10% chegou ao novo salário de R$ 1.196,25.

Como você pode perceber, partimos de um salário inicial e através de duas funções chegamos ao salário final.

Ainda utilizando tais funções, também podemos realizar os cálculos desta forma:

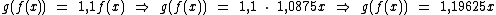
E como em nosso exemplo o salário inicial era de R$ 1.000,00, temos:

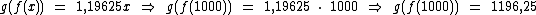
Fizemos uma composição de funções para, partindo de R$ 1.000,00, chegarmos aos R$ 1.196,25.

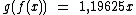é uma função composta.

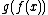também pode ser representada por .

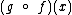Então a função composta de g em f seria:

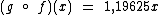
Generalizando a Composição de Funções

De uma forma geral, para duas funções definidas por 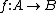e 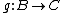, denominamos de função composta de g em f a função definida por 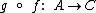, sendo 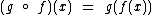, com .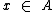

Representando a Composição de Funções no Diagrama de Flechas

Voltando ao nosso exemplo dos reajustes salariais, vamos dizer que tenhamos as seguintes definições de função:

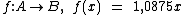
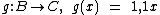
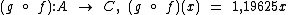
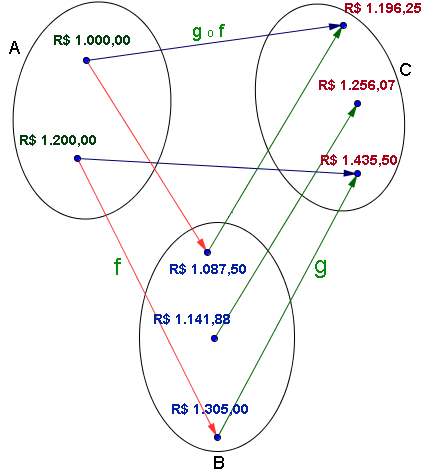
Agora vamos observar o diagrama de flechas à direita.

O conjunto A contém os valores iniciais dos salários e é o domínio das funções 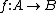e .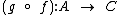

O conjunto B contém os salários após o primeiro reajuste. É também o contradomínio da função 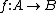e é o domínio da função .

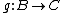O conjunto C contém os valores finais dos salários e é o contradomínio das funções 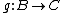e .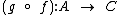

No caso da função 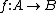, note que o elemento R$ 1.141,88, do conjunto B, não está relacionado a nenhum elemento do conjunto A. Incluímos esta situação apenas para que você recorde que segundo o conceito de função, podem sobrar elementos não associados no conjunto de chegada, mas nunca no conjunto de partida. Veja que no conjunto A todos os elementos estão relacionados a um, e somente um, elemento do respectivo conjunto de chegada.

Os valores do conjunto A foram escolhidos aleatoriamente como exemplo.

Os valores do conjunto B, com exceção do elemento R$ 1.141,88, que também foi escolhido aleatoriamente, foram obtidos através de :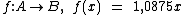

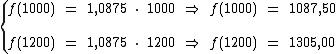
Os valores do conjunto C foram obtidos através :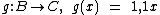

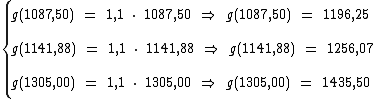
Os valores do conjunto C também podem ser obtidos através de 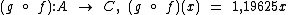, mas neste caso o elemento R$ 1.256,07 não é imagem de nenhum elemento de A:

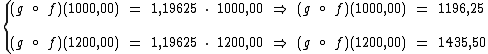
Normalmente f ^_o g ≠ g ^_o f

No começo deste artigo obtivemos a função g composta com f:

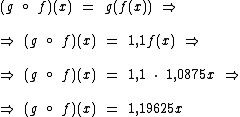
Mas também podemos obter a função composta f de g:

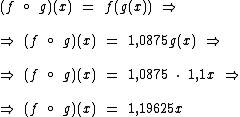
Note que neste caso 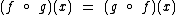, mas normalmente isto não ocorre.

Ocorreu neste caso, visto que ambas são funções lineares e como tais funções apenas multiplicam a incógnita x por um coeficiente real não nulo, a composição de f com g ou de g com f, não altera o resultado, pois como sabemos, a ordem dos fatores não altera um produto.

Outro Exemplo de Obtenção da Função Composta

Para encerrar este artigo vamos utilizar outras funções f e g e obter a composição de f com g e de g com f.

Utilizaremos as funções 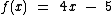e .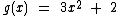

Primeiramente vamos obter :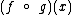

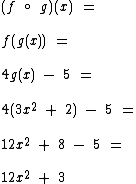
Agora vamos obter :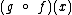

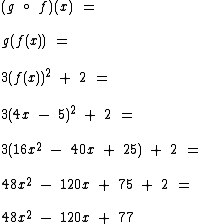
Neste caso você pode constatar que 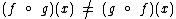, pois:

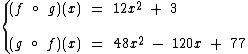
Para demonstrar que as composições equivalem a aplicação consecutiva de duas ou mais funções, vamos calcular f(10) e g(10), depois iremos calcular f(g(10)) e g(f(10) para finalmente confrontarmos estes dois últimos resultados com as composições acima e constatarmos que elas simplificam a aplicação das duas funções.

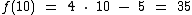
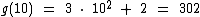
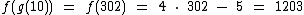
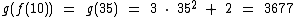
Agora vamos calcular as composições:

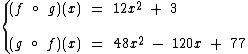
Substituindo x por 10 temos:

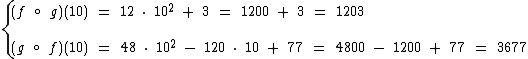
Como podemos observar, se calcularmos g(10) e sobre o valor obtido aplicarmos a função f, teremos o mesmo resultado que aplicarmos a função composta (f ^_o g)(10), ou seja, 1.203.

Com a aplicação inversa das funções, se calcularmos f(10) e sobre o valor obtido aplicarmos a função g, vamos obter o mesmo resultado que a aplicação da função composta (g ^_o f)(10), que vem a ser 3.677.