Equação do Primeiro Grau
Denomina-se equação do 1° grau com uma incógnita, qualquer equação que possa ser reduzida à forma ax = b, onde x é a incógnita e a e b são números reais, com a ≠ 0. a e b são coeficientes da equação.
Equações do 1° grau podem possuir mais de uma incógnita. Como exemplo, temos as equações do 1° grau com duas incógnitas, que são quaisquer equações que podem ser reduzidas a uma equação equivalente da forma ax + by = c, com a ≠ 0 e b ≠ 0. Neste caso, além de a e b, temos também c como coeficientes da equação.
Utilizamos equações do 1° grau com uma incógnita na resolução de problemas tal qual o seguinte:
"Se eu tivesse o dobro da quantia que eu possuo, com mais dez reais eu poderia comprar um certo livro que custa cem reais. Quantos reais eu possuo?"
Inicialmente iremos expressar este mesmo problema em linguagem matemática. Para isto vamos chamar a quantia que eu possuo atualmente de x. Este é valor procurado.
Ao referir-me ao dobro da quantia, matematicamente estou me referindo a 2x, ou seja, ao dobro de x.
O dobro da quantia mais dez reais será expresso matematicamente como 2x + 10.
Finalmente devemos expressar que o dobro da quantia mais dez é igual a cem, logo a expressão inteira será: 2x + 10 = 100.
Basicamente substituímos o texto em português pelos seus respectivos operadores matemáticos.
Resolução de equações do 1° grau com uma incógnita
Para solucionarmos a equação 2x + 10 = 100 iremos recorrer aos conceitos de equações equivalentes, princípio aditivo da igualdade e princípio multiplicativo da igualdade, vistos no tópico Equação. Resumindo, iremos obter equações equivalentes sucessivamente através da aplicação destes princípios, até que a raiz da equação seja encontrada.
Primeiramente vamos lembrar que o oposto de um número real é igual a este mesmo número com o sinal trocado. O oposto de 2 é igual a -2. Obviamente o oposto de -2 voltará ao número 2 inicial. Note ainda que a soma de um número pelo seu oposto sempre resultará em 0.
Precisamos também lembrar o que vem a ser o inverso de um número real diferente de zero. De antemão sabemos que um número real diferente de zero multiplicado pelo seu inverso resultará sempre em 1.
Segundo este conceito, o inverso de 2 é 1/2, já que 2 . 1/2 = 1. Obviamente o inverso de 1/2 é 2 pelo mesmo motivo.
O inverso de 3/5 é 5/3, pois 3/5 . 5/3 = 1.
Simplificando, se a for um número real inteiro e diferente zero, o seu inverso será 1/a. No caso de frações, o inverso multiplicativo da fração a/b será b/a, com a e b diferentes de zero.
A partir deste conceito podemos começar a solucionar a equação.
Vejamos:
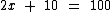
A ideia é deixarmos a incógnita x isolada no primeiro membro à direita do sinal de igualdade e a raiz no segundo membro, à esquerda. Gradualmente iremos passando os números do primeiro membro para o segundo membro.
Para passarmos o número 10 no primeiro membro, para o segundo membro, iremos recorrer ao princípio aditivo da igualdade. Vamos subtrair 10 dos dois membros da equação:
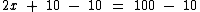
Ao subtrairmos 10 nos dois membros da equação, na verdade estamos somando o oposto de 10, que é -10 em ambos os membros como vemos abaixo, de sorte que o 10 saia do primeiro membro, pois como já vimos, ao somarmos um número real ao seu oposto o resultado sempre será igual a zero:
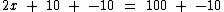
Ao realizarmos as operações chegaremos à equação:
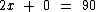
Que é equivalente a:
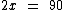
Para tirarmos o coeficiente 2 do primeiro membro, iremos recorrer ao princípio multiplicativo da igualdade, dividindo ambos os membros por 2:
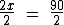
Na verdade o que estamos fazendo é multiplicando ambos os membros pelo inverso multiplicativo do coeficiente 2 que é 1/2, para que ele saia do primeiro membro, já que será reduzido ao número 1. Na realidade o cálculo seria este:
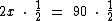
Realizando os cálculos em qualquer um dos dois casos encontramos a raiz procurada:
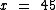
Passando para o outro lado
Depois de adquirido tais conhecimentos, podemos ver uma forma mais simples de solucionarmos este tipo de equação. Vejamos:
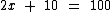
A ideia agora é passar o termo 10 do primeiro para o segundo membro. Como ele está sendo somado, passará para o outro lado sendo subtraído, já que a subtração é a operação inversa da adição:
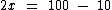
Que se resume a:
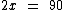
Passamos agora o coeficiente 2 para o segundo membro. Como ele está multiplicando, do outro lado ele estará dividindo. Isto porque a divisão é a operação inversa da multiplicação:
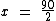
Realizando a divisão encontramos a raiz 45 encontrada anteriormente:
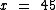
Apenas a título de verificação, vamos substituir a incógnita x por 45 para confirmarmos que este valor torna a equação verdadeira:
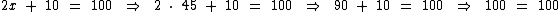
Resumo
Este método que acabamos de estudar resume-se em isolar a incógnita no primeiro membro, passando progressivamente cada um dos coeficientes para o segundo membro. A passagem é feita passando o termo para o outro lado, invertendo-se a operação que é realizada sobre o mesmo:
- Se for adição, passa a subtração;
- Se for subtração, passa a adição;
- Se for multiplicação, passa a divisão;
- Se for divisão, passa a multiplicação.
Na verdade tais inversões nada mais são que uma forma simplificada de utilização dos princípios aditivo e multiplicativo da igualdade, como visto inicialmente.
Exemplo de problema envolvendo a utilização de equação do primeiro grau
 O perímetro de um terreno retangular é de 200m. O terreno tem de largura 28m a menos que o seu comprimento. Qual é a área deste terreno?
O perímetro de um terreno retangular é de 200m. O terreno tem de largura 28m a menos que o seu comprimento. Qual é a área deste terreno?
Chamemos de x o comprimento do terreno, então x - 28 será a medida da sua largura. Sabemos que o perímetro de uma figura retangular é igual ao dobro da soma do seu comprimento com a sua largura. Matematicamente temos:
2 . (x + x - 28) = 200
Resolvendo a equação temos:
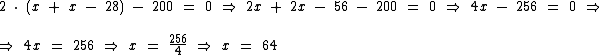
Então já temos que o comprimento do terreno é de 64m. Como de largura ele tem 28 metros a menos que isto, então ele tem 36m de largura.
Como sabemos, a área do terreno será obtida multiplicando-se a medida do seu comprimento, pela medida da sua largura, portanto:
 A área deste terreno é de 2304m2.
A área deste terreno é de 2304m2.
