Plano Cartesiano
O Plano Cartesiano foi criado pelo matemático René Descartes. Como ele associava a geometria à álgebra, esta foi a forma que ele criou para representar graficamente expressões algébricas.
A sua utilização mais simples é a de representarmos graficamente a localização de pontos em um determinado plano. Através dele também podemos representar um segmento de reta ou um triângulo, por exemplo.
O plano cartesiano é composto de duas retas perpendiculares e orientadas, uma horizontal e outra vertical.
Damos no nome de eixo x ou eixo das abscissas à reta horizontal. À vertical denominamos de eixo y ou eixo das ordenadas.
A orientação positiva das retas é representa por uma seta como podemos ver na figura mais abaixo.
Representação de Pontos no Plano Cartesiano
A representação de pontos neste plano é feita através de pares ordenados, onde o primeiro número se refere à abscissa e o segundo a ordenada.
O ponto P1(3, 2) tem abscissa 3 e ordenada 2, no qual o símbolo (3, 2) representa um par ordenado. O ponto P2(2, 3) tem abscissa 2 e ordenada 3. É importante frisarmos que os pontos P1 e P2 são pontos distintos, pois em um par ordenado a ordem dos números é relevante.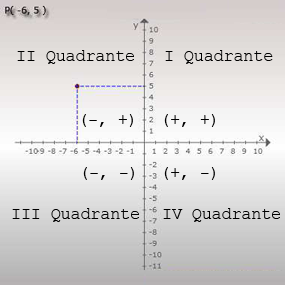
Dois pares ordenados (a, b) e (c, d) são iguais se e somente se a = c e b = d.
Na figura ao lado vemos a representação do ponto P(-6, 5).
Ao ponto localizado no cruzamento de ambos os eixos damos o nome de origem do sistema de coordenadas cartesianas, representado por O(0, 0).
Quadrantes do Plano Cartesiano
Vemos nesta figura que o eixo x e o eixo y dividem o plano em quatro regiões. A região do canto superior direito é o primeiro quadrante, a região à sua esquerda, do outro lado do eixo y é o segundo quadrante. Abaixo deste temos o terceiro quadrante e à sua direita, ou seja, abaixo do primeiro temos o quarto quadrante.
Os quadrantes são dispostos em sentido anti-horário.
Sinal da Abscissa e da Ordenada de um Ponto
Todos os pontos no primeiro quadrante possuem abscissa e ordenada positivas. Exemplo: P1(3, 5).
No segundo quadrantes todos os pontos possuem abscissa negativa e ordenada positiva. Exemplo: P2(-4, 2).
Todos os pontos no terceiro quadrante possuem abscissa e ordenada negativas. Exemplo: P3(-7, -1).
No quarto quadrante todos os pontos possuem abscissa positiva e ordenada negativa. Exemplo: P2(8, -3).
Note que os três pontos abaixo não se encontram em nenhum quadrante, pois eles estão localizados sobre o eixo x, o eixo y e a origem do sistema, respectivamente:
 P(-1, 0)
P(-1, 0)
 P(0, -2)
P(0, -2)
 P(0, 0)
P(0, 0)
