Números Imaginários

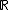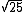No conjunto dos números reais ( ) a é igual a 5, mas qual é a ?

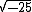Como sabemos, não existe a raiz quadrada real de um radicando negativo com índice par. No conjunto dos números reais o máximo que podemos fazer é simplificar o radical desta forma:

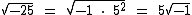
Ainda assim o fator 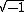não é um número real, pois o radicando -1 é um número negativo.

Para maiores informações sobre como retiramos o número 5 do radical, você pode consultar o nosso artigo sobre a radiciação e suas propriedades.

Unidade Imaginária

A solução para este tipo problema surgiu com a criação dos números imaginários, cuja unidade imaginária representada pela letra i, é igual a .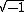

Utilizando-se do conceito de número imaginário podemos dizer que a 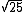é igual a 5i, pois:

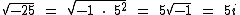
Agora vamos solucionar a equação do segundo grau abaixo:

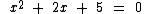
O primeiro passo é calcularmos o seu discriminante:

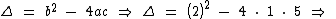
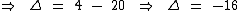
Como o discriminante é negativo, a equação não possui raízes reais:

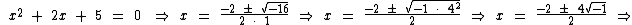
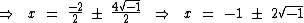
Mas possui raízes imaginárias ao substituirmos 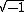por i:

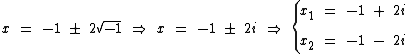
Nos dois exemplos acima, 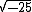e 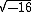, temos um radicando que é o valor simétrico de um quadrado perfeito, ou seja, o oposto de 25 e de 16, que são quadrados perfeitos, mas mesmo que não o fossem, ainda assim poderíamos trabalhar com o conceito de números imaginários.

Vejamos o exemplo do número :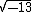

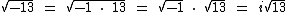
Observe que não eliminamos o radical, pois o número 13 não é um quadrado perfeito, mas agora temos um radicando positivo.

Quadrado perfeito é qualquer número inteiro maior ou igual a zero, que podemos representar pelo quadrado de um número também inteiro, por exemplo, 144 é um quadrado perfeito, pois: 144 = 12²

Há casos em que alguns fatores do número saem do radical e outros fatores não. Veja o exemplo do número :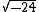

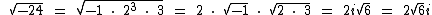
Números Complexos

Ao estudarmos os conjuntos numéricos fundamentais vimos que os números racionais podem ser expressos na forma de uma fração, com numerador e denominador inteiros e com denominador diferente de zero:

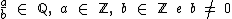
De forma semelhante os números complexos podem ser representados por meio de uma expressão algébrica:

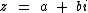
Sendo a e b números reais e i a unidade imaginária.

a é a parte real do número complexo z e bi é a sua parte imaginária.

Definimos o conjunto dos números complexos como:

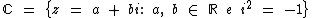
O conjunto dos números reais ( 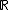) e o conjunto dos números imaginários ( 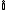) são subconjuntos do conjunto dos números complexos ( 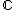). Em função disto um número complexo pode ser imaginário, imaginário puro ou real.

Exemplos de Números Imaginários

Para a ≠ 0 e b ≠ 0 temos um número imaginário:

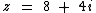
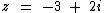
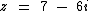
Como podemos observar um número imaginário possui uma parte real e outra imaginária.

Exemplos de Números Imaginários Puros

Para a = 0 e b ≠ 0 temos um número imaginário puro:

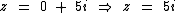
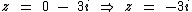
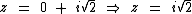
Números imaginários puros possuem apenas a parte imaginária.

Exemplos de Números Reais

Para a ≠ 0 e b = 0 temos um número real:

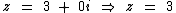
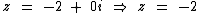
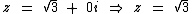
Números reais não possuem a parte imaginária.

Conjugado de um Número Complexo

O conjugado de um número complexo 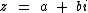é o número complexo .

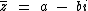Observe que tanto z, quanto o seu conjugado possuem a mesma parte real, mas as partes imaginárias são opostas. Quando ambas as partes, real e imaginária, são iguais, os números também o são. A igualdade só ocorre nestas condições.

As raízes imaginárias x₁ e x₂ da equação x² + 2x + 5 = 0, solucionada mais acima, são conjugadas uma da outra:

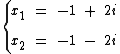
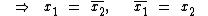
Exemplos de Números Complexos e seu Conjugado

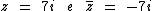
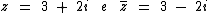
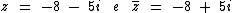
Conjuntos Numéricos em Diagrama

No diagrama abaixo observamos que o conjunto dos números reais ( ) é um subconjunto do conjunto dos números complexos ( ).

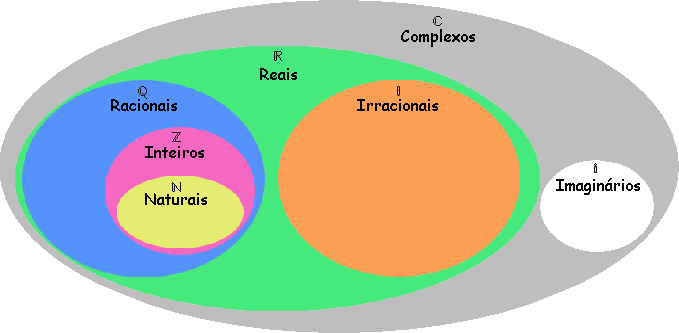
Através deste diagrama podemos concluir que todo número real é complexo, mas nem todo número complexo é real, pois um número complexo pode possuir uma parte imaginária, mas os números reais não a possuem.