Resolução de Equações Algébricas
Há muitas páginas neste site que resolvem problemas através do uso de equações algébricas. A maioria delas pressupõe que você saiba como solucionar estas equações.
Algumas outras dão algumas informações básicas sobre o tema e a página equação do primeiro grau trata o assunto mais detalhadamente.
Por se tratar de uma matéria muito importante, ainda que haja uma outra página específica sobre o tema, esta página foi criada para mais uma vez procurarmos explicar como devemos proceder para solucionar tais equações.
Identificando as Partes de uma Equação Algébrica
Vamos analisar a equação algébrica abaixo:
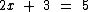
Ela possui dois membros. O primeiro membro é o que está à esquerda do sinal de igualdade, ou seja, é 2x + 3.
Este membro possui dois termos. São eles 2x e 3. Estes termos são as duas parcelas de uma soma.
O primeiro termo do primeiro membro, 2x, é formado pelo coeficiente numérico igual a 2 e pela parte literal x, a incógnita da equação. O segundo termo não possui a parte literal, é formado apenas pelo número real 3.
Incógnita ou variável é a grandeza a ser determinada na solução de uma equação.
Na página sobre termos algébricos você encontra maiores informações sobre coeficiente numérico e parte literal, dentre outras.
O segundo membro está à direita do sinal de igualdade, possui apenas um termo sem a parte literal. É o número real 5.
O que Vem a Ser "Solucionar uma Equação Algébrica"?
Solucionar uma equação algébrica é identificar o valor numérico da incógnita, que ao ser substituída na equação torna-a verdadeira.
Na equação do nosso exemplo, 1 é o valor que substituindo a incógnita x torna a equação verdadeira, logo x é a sua solução.
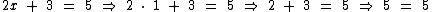
Para solucionarmos uma equação, executamos uma série de operações em ambos os seus membros, para sempre mantermos a condição de igualdade. São estas as operações que tratamos nesta página.
Principais Operações Utilizadas na Resolução de Equações Algébricas
Nosso objetivo é isolarmos no primeiro membro a incógnita, obtendo assim no segundo membro a solução da equação.
Voltando ao nosso exemplo, em busca de nosso objetivo de deixar a incógnita isolada, vamos eliminar o segundo termo do primeiro membro.
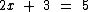
Como conseguí-lo?
Adicionar um Determinado Valor a Ambos os Membros da Equação
Como queremos eliminar o termo 3, que está sendo somado ao termo 2x, vamos subtrair 3 de ambos os membros:
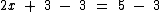
Como 3 - 3 = 0, eliminamos assim o termo 3.
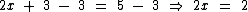
E se o mesmo estivesse sendo subtraído de 2x, em vez de estar sendo somado?.
Subtrair um Determinado Valor de Ambos os Membros da Equação
Neste caso a nossa equação exemplo seria:
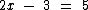
Como 3, está sendo subtraído de 2x, precisamos somar 3 a ambos os membros:
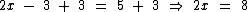
Apenas para ressaltar, a operação precisa ser realizada em ambos os termos da equação para que a condição de igualdade seja mantida.
Multiplicar Ambos os Membros da Equação por um Determinado Valor
Vejamos a equação abaixo:
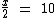
Como objetivamos isolar no primeiro membro a incógnita x, uma forma de fazê-lo é multiplicarmos ambos os membros por 2:
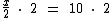
Ao realizarmos tal operação podemos simplificar o denominador da fração com o multiplicador 2, realizando assim a eliminação desejada:
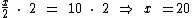
Escolhemos como multiplicador exatamente o denominador da fração, para podermos realizar a simplificação, eliminando o denominador e isolando a variável x.
Dividir Ambos os Membros da Equação por um Determinado Valor
Agora vejamos a equação a seguir:
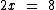
O objetivo continua o mesmo, isolarmos a variável x.
Sabemos que dividindo qualquer número, diferente de zero, por ele mesmo obteremos a unidade com resultado. Então vamos dividir ambos os membros por 2:
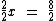
Realizando a simplificação temos:
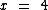
Realizar Multiplicação Distributiva
A propriedade distributiva da multiplicação é uma ferramenta muito útil na busca do isolamento da incógnita. Vamos estudar a equação abaixo:
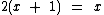
Qualquer uma das quatro operações estudadas acima, não nos auxilia na resolução desta equação, no entanto podemos distribuir o 2 que está em evidência, como abaixo:
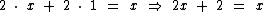
Agora podemos utilizar algumas das operações citadas anteriores para concluirmos a resolução.
Primeiro vamos subtrair x de ambos os membros da equação:
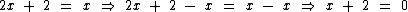
Finalmente subtraímos 2 dos dois lados:
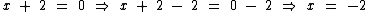
Fatoração
Em algumas situações ao invés da distribuição, precisamos fazer uma fatoração, colocando um termo comum em evidência. Normalmente temos tal necessidade quando há mais de uma variável na equação.
Vejamos neste outro exemplo como isolar a variável x na seguinte equação:
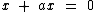
Note que x é um fator comum aos dois termos do primeiro membro.
Colocá-lo em evidência significa que vamos reescrever tal equação na forma de um produto, onde x será um dos fatores e o outro fator será formado pela soma dos dois termos divididos por x.
Como x dividido por x é igual a 1 e ax dividido por x é igual a a, temos:
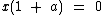
Agora para encontrarmos o valor de x, basta dividirmos os dois termos da equação por (1 + a).
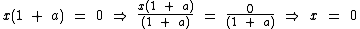
Vejamos outros exemplos de fatoração:

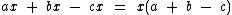

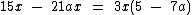

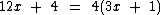

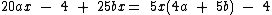
Observe que tanto no caso da propriedade distributiva, quanto no caso da fatoração, não foi preciso realizarmos a mesma operação em ambos os membros da equação, agimos só de um lado, pois tais operações não "desequilibram" a equação.
Permutar um Membro com o Outro
A qualquer momento podemos mudar os membros de lado. Se, por exemplo, após a realização de algumas operações chegarmos a algo como:
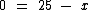
Podemos trocar os membros de lado, o que não causará desequilíbrio na equação:
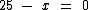
Isolando Variáveis em Fórmulas de Matemática Financeira
Agora para exemplificar a utilização de tais operações em uma situação mais concreta, vamos brincar um pouco de isolar variáveis de algumas fórmulas da matemática financeira envolvendo juros simples.
Na verdade vamos brincar com duas fórmulas, a do montante e a dos juros simples. Vamos unir as duas fórmulas em uma única equação e depois isolarmos cada uma das suas variáveis.
Como sabemos, a fórmula do montante em juros simples é:
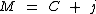
Já a fórmula dos juros simples é:
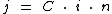
Se você não se lembra a que se referem cada uma das variáveis envolvidas nas fórmulas acima, você pode acessar a página que trata sobre juros simples, ou então continuar a leitura desta página, pois iremos isolar cada uma das incógnitas e você verá do que elas se tratam. Na referida página, porém, você encontra maiores informações.
Na fórmula do montante queremos isolar a variável C, que se refere ao capital aplicado ou valor principal. Como fazê-lo?
Isolando a Variável "C" na Fórmula do Montante
Neste caso precisamos eliminar a variável j, no segundo membro, somada a C.
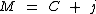
Para isto iremos subtrair a mesma incógnita j de ambos os membros:
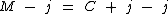
Como j - j = 0, então:
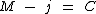
Agora é só trocarmos os membros de lado:
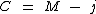
Agora vamos substituir C por M - j na fórmula do juro simples, fundido as duas fórmulas em uma só:
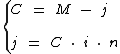
Então, após a substituição de C:
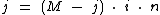
Podemos escrever esta mesma fórmula omitindo os operadores de multiplicação, que ficará como:
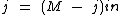
Está é a fórmula que usaremos na brincadeira.
Isolando a Variável "j"
Esta variável representa os juros da aplicação. Note que na referida fórmula ela ocorre duas vezes. Este é o caso mais complexo que iremos tratar aqui.
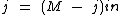
Nossa primeira providência será aplicarmos a propriedade distributiva, multiplicando M e j, que estão entre parênteses, por in:
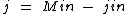
Tomamos esta medida, pois agora podemos somar jin nos dois lados, o que não resolveria inicialmente, de sorte a eliminarmos jin no segundo membro e de só haver termos com j no primeiro membro:
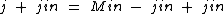
Logo:
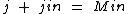
Vamos agora colocar j em evidência, para que possamos eliminar o outro fator, isolando j.
Como j dividido por j é igual a 1 e jin dividido por j é igual a in, temos:
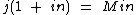
Finalmente podemos isolar j dividindo ambos os membros por 1 + in:
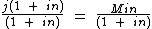
Simplificando 1 + in do numerador, com 1 + in do denominador no primeiro membro, temos:
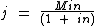
Isolando a Variável "M"
Isolar o Montante é bem mais simples.
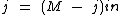
Como M - j está sendo multiplicado por in, que impede tanto M, quanto j de serem manipulados separadamente, vamos dividir os dois lados da equação por in, o que irá extinguir tal restrição, já que in será eliminado do segundo membro:
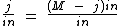
Simplificando temos:
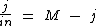
Agora não tem mais segredo, para isolarmos M simplesmente somamos j nos dois lados:
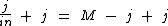
Portanto:
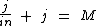
Podemos inverter os membros da equação:
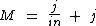
Como j ocorre duas vezes, vamos colocá-lo em evidência dividindo por j, tanto j/in que dá 1/in, quanto j que dá 1:
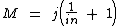
Isolando a Variável "M" de Outra Forma
Da maneira que fizemos anteriormente é mais simples, mas também podemos proceder como se fossemos isolar j, realizando as operações até este ponto:
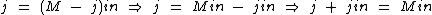
Vamos inverter os membros da equação para deixar M no primeiro membro:
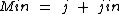
É fácil percebemos que devemos dividir os dois membros por in para isolarmos M:
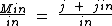
Que simplificando resulta em:
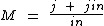
Como in ocorre no numerador e no denominador, podemos realizar uma simplificação se separarmos as duas parcelas da adição:
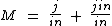
Simplificando fica:
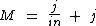
Então colocamos j em evidência exatamente como fizemos anteriormente pela outra forma de isolarmos M:
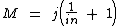
Isolando a Variável "i"
Se você conseguiu assimilar a maior parte do que foi explicado até aqui, é muito provável que você já saiba como isolar a taxa de juros.
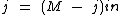
Inicialmente vamos inverter os membros de lado:
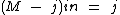
Como no primeiro membro temos uma multiplicação com três fatores, basta dividirmos os dois lados por todos os fatores que pretendemos eliminar no primeiro membro, ou seja, temos que dividir os dois membros por (M - j)n:
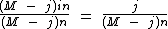
Que após a simplificação fica igual a:
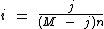
Isolando a Variável "n"
O período de tempo da aplicação é isolado de forma análoga ao isolamento da taxa de juros.
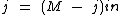
Iniciamos invertendo os membros da equação:
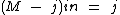
Dividimos os dois membros por (M - j)i para eliminarmos tais fatores do primeiro membro:
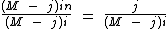
Simplificando finalmente temos:
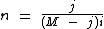
Se você ainda estiver com dúvidas, talvez ajude se você voltar ao início do texto e ir tentando resolver os exemplos escrevendo-os no papel.
Aqui, para o isolamento das variáveis nos fundamentamos nos princípios da igualdade, realizando uma mesma operação em ambos os membros de uma igualdade, de forma a mantê-la.
Se você estiver mais familiarizado com o método de passagem de termos de um lado para ou outro, através da realização da operação inversa e da mudança de sinal, talvez o texto contido na página sobre equação do primeiro grau lhe seja de maior valia, pois lá falamos um pouco desta metodologia.
O artigo cálculos algébricos também pode lhe interessar. Nele temos a resolução de um problema tanto em termos aritméticos, quanto em termos algébricos.
