Fração Geratriz
A representação da fração 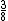 em números decimais é 0,375, assim como a representação decimal da fração
em números decimais é 0,375, assim como a representação decimal da fração 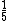 é 0,2.
é 0,2.
Repare que embora o número de casas decimais em cada um dos exemplos seja diferente, eles são finitos. O primeiro exemplo possui três casas decimais, ao passo que o segundo exemplo possui apenas uma.
Agora qual seria a representação decimal da fração 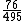 ?
?
Note que neste caso o número de casas decimais da representação desta fração na forma decimal, não será um número finito. 76 dividido por 495 será algo como 0,1535353...
Se continuarmos o processo de divisão, iremos indefinidamente acrescentar um dígito 5, depois um 3, depois um 5 e assim por diante, sendo que sempre poderemos continuar acrescentando mais um dígito. A isto damos o nome de dízima periódica
As dízimas periódicas podem ser simples ou composta, no caso do exemplo acima temos uma dízima periódica composta.
A dízima periódica composta 0,1535353... foi gerada a partir da fração 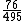 , por isto esta fração é chamada de fração geratriz da dízima periódica.
, por isto esta fração é chamada de fração geratriz da dízima periódica.
Classificando as Dízimas Periódicas em Simples e Compostas
A dízima periódica 0,1535353... é composta, pois ela possui um anteperíodo que não se repete, no caso o número 1, e um período formado pelo número 53, que se repete indefinidamente. Se fosse apenas 0,535353... teríamos uma dízima periódica simples, pois ela possui apenas um período, 53, mas não um anteperíodo.
Veja abaixo alguns exemplos:
Exemplos de Dízimas Periódicas Simples
0,111... período igual a 1
0,252525... período igual a 25
0,010101... período igual a 01
0,123123123... período igual a 123
Exemplos de Dízimas Periódicas Compostas
0,2333... anteperíodo igual a 2 e período igual a 3
0,45222... anteperíodo igual a 45 e período igual a 2
0,171353535... anteperíodo igual a 171 e período igual a 35
0,32101230123... anteperíodo igual a 32 e período igual a 0123
Transformando Dízimas Periódicas Simples em Frações Geratrizes
Um método prático para se obter a fração geratriz no caso de dízimas periódicas simples, consiste em utilizarmos o período como numerador e utilizarmos como denominador um número formado por tantos dígitos 9, quantos forem os dígitos do período. Vejamos:
0,111... 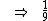
0,252525... 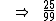
0,010101... 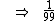
0,123123123... 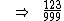
Repare no último exemplo que o numerador 123 e o denominador 999 não são primos entre si, de fato o seu máximo divisor comum não é 1, mas sim 3. Realizando a simplicação de ambos os termos por 3, a fração 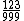 será transformada na fração irredutível equivalente
será transformada na fração irredutível equivalente 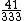 .
.
Caso a dízima possua uma parte inteira, basta a destacarmos e calcularmos a parte decimal como já explicado:
5,7373... 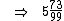
Note que 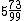 é uma fração mista que pode ser transformada na fração imprópria
é uma fração mista que pode ser transformada na fração imprópria 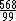 .
.
Transformando Dízimas Periódicas Compostas em Frações Geratrizes
Em função da existência de um anteperíodo, neste caso a técnica é ligeiramente diferente. Veja o exemplo abaixo:
0,171353535... 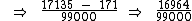
O número 17135 é formado pela junção do anteperíodo, 171, com o período, 35. Ao subtrairmos deste número o anteperíodo, obtemos 16964, o numerador da fração geratriz. O denominador é formado por tantos dígitos 9, quantos são os dígitos do período, assim como no caso das dízimas periódicas simples, seguidos de tantos dígitos 0, quantos são os dígitos do anteperíodo.
A fração 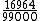 é passível de simplificação. Como o maior divisor de ambos os termos é quatro, a fração irredutível será
é passível de simplificação. Como o maior divisor de ambos os termos é quatro, a fração irredutível será 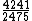 .
.
Veja abaixo mais alguns exemplos:
0,2333... 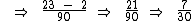
0,45222... 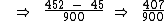
0,888313131... 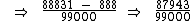
0,32101230123... 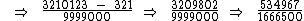
17,16151515... 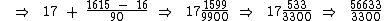
Acesse também a Calculadora de Frações Geratrizes que obtém a fração geratriz a partir de uma dízima periódica.
