Regra de Três
A resolução de problemas que envolvem grandezas proporcionais pode ser realizada através de uma regra prática denominada "regra de três".
Se tivermos duas grandezas diretamente proporcionais, utilizaremos a "regra de três simples direta" e caso elas sejam inversamente proporcionais, utilizaremos a "regra de três simples inversa".
Nos problemas onde temos três ou mais grandezas, utilizamos a "regra de três composta". Observe que neste caso, um mesmo problema pode envolver tanto grandezas diretamente proporcionais, quanto grandezas inversamente proporcionais.
Regra de Três Simples Direta
 Uma pessoa recebe R$ 1.800,00 por 30 dias trabalhados. Quantos dias esta pessoa precisará trabalhar para ter direito a receber R$ 1.200,00?
Uma pessoa recebe R$ 1.800,00 por 30 dias trabalhados. Quantos dias esta pessoa precisará trabalhar para ter direito a receber R$ 1.200,00?
Este é o típico caso da utilização de uma "regra de três simples direta". Simples por envolver apenas duas grandezas proporcionais, e direta, porque quando uma grandeza aumenta, a outra também aumenta. Se uma diminui, o mesmo ocorre com a outra.
Chamemos de S a grandeza que representa o salário e de D a grandeza que representa o número de dias de trabalho e vejamos a representação abaixo:
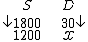
As setas apontam na mesma direção, pois as grandezas são diretamente proporcionais. Percebemos isto, pois ao diminuirmos o número de dias trabalhados, também teremos o respectivo salário diminuído. Como o salário vai ser reduzido, obviamente o número de dias de trabalho também será. Concluímos assim, que as grandezas S e D são diretamente proporcionais.
De acordo com a orientação das setas, podemos então montar a proporção:
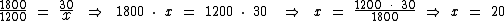
 Concluímos que para ter o direito a receber os R$ 1.200,00, a pessoa terá que trabalhar por 20 dias.
Concluímos que para ter o direito a receber os R$ 1.200,00, a pessoa terá que trabalhar por 20 dias.
Como você pode notar, a resolução de um problema de regra de três, tem por base a "propriedade fundamental das proporções". Veja mais sobre isto em proporção.
Regra de Três Simples Inversa
 Dois pedreiros trabalhando juntos conseguem construir um certo muro em 6 horas de trabalho. Se ao invés de dois, fossem três pedreiros, em quantas horas tal muro poderia ser construído?
Dois pedreiros trabalhando juntos conseguem construir um certo muro em 6 horas de trabalho. Se ao invés de dois, fossem três pedreiros, em quantas horas tal muro poderia ser construído?
Você pode facilmente compreender que aumentando o número de pedreiros, o tempo necessário para a construção do muro será menor, pois a mão de obra aumenta, mas a tarefa continua a mesma.
Percebemos então que este problema trata grandezas inversamente proporcionais, ou seja, quando uma grandeza aumenta, a outra diminui e vice-versa.
Vamos chamar de P a grandeza que representa a quantidade de pedreiros e de H a grandeza que representa o número de horas de trabalho para a construção do muro. Vejamos então a representação abaixo:
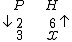
Neste caso as setas apontam na direção oposta, pois as grandezas são inversamente proporcionais.
Para a resolução do problema, iremos novamente utilizar a "propriedade fundamental das proporções", no entanto para que isto seja possível, devemos primeiro deixar as duas setas com a mesma orientação. Como a seta referente à grandeza H (a grandeza referente ao x) está para cima, iremos inverter os termos da outra razão para que a sua seta também fique para cima:
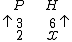
Perceba que sempre que tenhamos que realizar alguma mudança na orientação das setas, a grandeza que contém o termo x é tomada como referência e não é alterada. A outra grandeza, ou outras no caso de se tratar de uma regra de três composta, é que deve mudar.
Então agora podemos montar a proporção segundo a "propriedade fundamental das proporções":
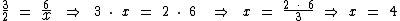
 Portanto com três pedreiros serão necessárias apenas 4 horas de trabalho.
Portanto com três pedreiros serão necessárias apenas 4 horas de trabalho.
Regra de Três Composta
 Uma pessoa consome 4000 litros de água por mês. Quantos litros de água duas pessoas irão consumir em um ano?
Uma pessoa consome 4000 litros de água por mês. Quantos litros de água duas pessoas irão consumir em um ano?
Primeiramente para facilitar a explicação, iremos atribuir uma letra a cada grandeza. Sejam elas:
- P: O número de pessoas;
- L: A quantidade de litros de água;
- T: O período de tempo envolvido.
Montemos a representação para analisarmos o problema, mas no lugar de um ano, iremos utilizar doze meses, para que os dois períodos de tempo fiquem na mesma unidade de medida:
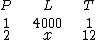
A ordem de colocação das grandezas na representação acima, é a mesma que a do enunciado do problema. Como você pode perceber, a grandeza L, que é a grandeza que estamos procurando (a grandeza que contém o termo x), não está posicionada nem à direita, nem à esquerda do diagrama. Isto é uma má ideia, pois irá dificultar em muito a resolução do problema, por isto devemos passá-la para a extremidade direita, ou para a esquerda. Vamos escolher esta última:
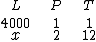
Agora ficou melhor, vamos então identificar a orientação das setas, ou em outras palavras, determinar se as grandezas são diretamente ou inversamente proporcionais entre si.
A grandeza de referência é a grandeza L. A posição da sua seta pode ser arbitrada tanto para cima, quanto para baixo, tanto faz. Vamos escolher para baixo:
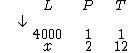
Agora vamos determinar se L e P são diretamente proporcionais ou não. Sabemos que uma pessoa consome 4000 litros. Como mais pessoas irão consumir mais litros, então as grandezas são diretamente proporcionais, logo a seta de P terá a mesma orientação da seta de L, ou seja, também para baixo:
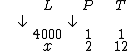
Finalmente falta-nos determinar se L e T são diretamente ou inversamente proporcionais. Sabemos que em um mês são consumidos 4000 litros. Obviamente se aumentarmos o tempo de consumo, também aumentaremos o consumo em litros, então as grandezas são diretamente proporcionais, logo a seta de T terá a mesma orientação da seta de L, isto é, para baixo:
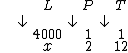
Se houvesse alguma seta com orientação oposta à seta de L, os termos desta grandeza deveriam ser invertidos. Como não é o caso, basta-nos montarmos a proporção e resolvê-la:
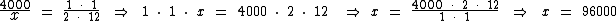
 Portanto as duas pessoas irão consumir 96 mil litros de água em um ano. A título de curiosidade, 96000 litros equivalem a 96 metros cúbicos.
Portanto as duas pessoas irão consumir 96 mil litros de água em um ano. A título de curiosidade, 96000 litros equivalem a 96 metros cúbicos.
 Para encher um tanque com 400 metros cúbicos de capacidade, duas torneiras levaram 4 horas para enchê-lo. Quantas horas seriam necessárias para enchê-lo com 6 torneiras, se o tanque tivesse apenas 300 metros cúbicos de capacidade?
Para encher um tanque com 400 metros cúbicos de capacidade, duas torneiras levaram 4 horas para enchê-lo. Quantas horas seriam necessárias para enchê-lo com 6 torneiras, se o tanque tivesse apenas 300 metros cúbicos de capacidade?
Primeiro vamos atribuir uma letra a cada grandeza:
- M: A capacidade em metros cúbicos do tanque;
- T: A quantidade de torneiras;
- H: A duração de cada operação em horas.
A representação para analisarmos o problema é a seguinte:
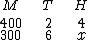
Observe que na montagem a grandeza H, que é a grandeza que estamos procurando (a grandeza que contém o termo x), deve estar posicionada à direita, como colocamos, ou à esquerda se desejássemos, mas não em outra posição. O motivo disto é deixar a razão com o termo x isolada.
A partir daí podemos então identificar a orientação das setas, ou em outras palavras, determinar se as grandezas são diretamente ou inversamente proporcionais entre si.
A grandeza de referência é a grandeza H, pois é ela que está sendo procurada. Você já sabe que a posição da sua seta pode ser arbitrada tanto para cima, quanto para baixo. Para padronizar, vamos escolher a seta da grandeza de referência sempre para baixo:
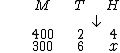
Vamos determinar se H e M são diretamente proporcionais ou não. Sabemos que ao diminuirmos a capacidade do tanque, também iremos diminuir o tempo necessário para enchê-lo, então em sendo assim, as duas grandezas são diretamente proporcionais, logo a seta de M terá a mesma orientação da seta de H que é para baixo:
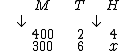
Vamos agora determinar se T e H são diretamente ou inversamente proporcionais. Sabemos que se aumentarmos a quantidade de torneiras, automaticamente iremos diminuir o tempo necessário para encher o tanque, por isso as duas grandezas são inversamente proporcionais, logo a seta de T terá orientação oposta a da seta de H, ou seja, será para cima, pois quanto uma aumenta a outra diminui:
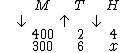
Podemos perceber que a seta da grandeza T possui orientação oposta à da grandeza H, devemos então inverter tanto a seta, quanto os seus elementos. Teremos então:
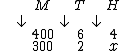
Por fim montemos a proporção e vamos resolvê-la seguindo a "propriedade fundamental das proporções":
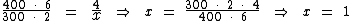
 Portanto com 6 torneiras poderíamos encher 300 metros cúbicos em apenas uma hora.
Portanto com 6 torneiras poderíamos encher 300 metros cúbicos em apenas uma hora.
